This post is for anyone taking linear algebra or wants to understand why they hated taking it.

I’m taking a graduate level linear systems analysis course that’s meant to serve as a primer to things like non-linear systems and advanced control theory, and I’ve been having flashbacks to what I think is one of the most poorly constructed/taught subjects: linear algebra.

Linear algebra is an amazing subject because its entire purpose is to greatly simplify huge complex problems to a couple matrix operations that can be shredded by a computer in fractions of a second. Solving one differential equation is a pain, solving several is nigh impossible. But then it turns out you can just take the coefficients, throw them into a matrix on your calculator, and boom problem solved. So why is it such a hard class? At my school, way more people failed linear algebra than any other math class.

Two reasons that are intertwined. The first reason is that linear algebra is often the class where they introduce all the formal math notation that looks like hieroglyphs. The “text” below is a completely logical and legitimate sentence in math:

It’s….a lot. 10 points to whoever can translate it into English. The second reason is because of a philosophical difference between mathematicians and engineers. Mathematicians have a thousand rules and definitions, and no exceptions. Engineers have a couple rules, and a thousand exceptions.

If mathematicians see a situation and the rule doesn’t *exactly* apply, they invent a new more general rule and create another theorem and definition or term. Engineers will just look at the error caused by following the rule, and add it to a look-up table. Math is about precisely pulling out patterns with a combo of abstractions and rigor. But it all lives on the page, in the abstract, so definitions and rules are free to make. It costs nothing to write a theorem. This is not true of engineering. The point of engineering is to leap off the page, out of our minds, and into reality. Reality is so complex that if you sit around looking for the exact right equation or algorithm to apply, you’ll never get anywhere.

This difference leads to linear algebra being *stuffed* with dozens of definitions, and just as you’re finally understanding the last set you get another set thrown at you. I had a hard time with it until toward the end when I noticed a pattern, and then it all clicked. I shall pass that wisdom onto you, let me demystify it for you in a way that is sure to piss off mathematicians.

Below are two vectors. They are perpendicular to each other.

Below are two vectors. They are orthogonal to each other.

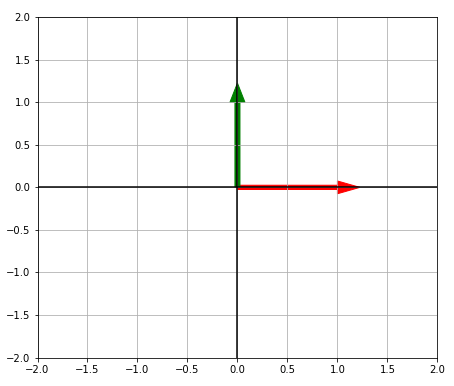
Below are two vectors. They are linearly independent to each other.

Below are two vectors. They are normal to each other.

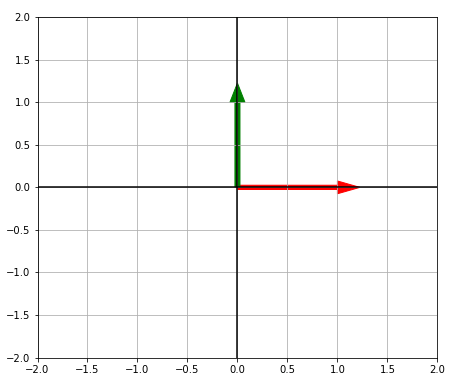
Do you see the pattern here? I’m not saying those terms all mean the same thing, but they’re similar and related enough that in most of the practical situations they do. The trick to understanding linear algebra is understanding that half the words mean almost the same thing. So every time you encounter a new term or definition, first try and connect it to something you already learned. It’ll make the class 10 times easier.

• Uncategorized